The Group Law

The group law for elliptic curves states three points on a curve E sum to the zero (i.e., O = [0, 1, 0] at infinity in projective geometry). Let P, Q \in E, then the line through P and Q (if P=Q, then we use the tangent line at P) intersects E at another point R. The line through R and O intersects E at P + Q.

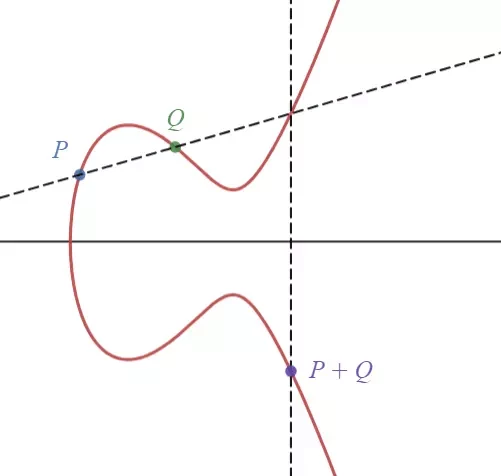
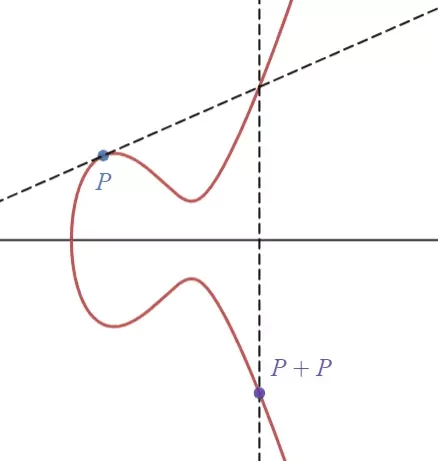
In this group, O is the identity element and the inverse of P=[x,y,z] is -P=[x,-y,z]. Note this group is abelian. You may prove the commutativity and associativity by yourself.

Let n \in \mathbb N. We define [0]P = O, [n]P = \underbrace{P + \cdots + P}_{n\text{ terms}}, and [-n]P = -[n]P. We call n the order of P if it is the smallest positive integer satisfies [n]P = O.

Why Are ECC Keys Shorter Than RSA Keys?

Assuming G is a group and a,b \in G. Discrete logarithm problem (DLP) is the problem of finding x \in \mathbb N such that a^x=b. For any group, we need at most O(\sqrt{|G|}) steps to solve the DLP. The ease of solving DLP can vary among different groups. For example,

1. In the additive group of a finite field \mathbb Z/p, we can use Euclidean algorithm to solve the DLP in O(\log p) steps.

2. In the multiplicative group of a finite field \mathbb F_p, we can solve the DLP in \exp(c\sqrt[3]{(\log p)(\log \log p)^2}) steps (c is a constant).

3. In an elliptic curve E(\mathbb F_p), the best known algorithm solves DLP in O(\sqrt p) steps.

Because the DLP in an elliptic curve group is much harder, ECC keys are usually shorter than RSA keys.

Elliptic Curve Diffie–Hellman (ECDH) Key Exchange

Alice and Bob agree on a field \mathbb F_p, and elliptic curve E over the field \mathbb F_p, and a point P \in E(\mathbb F_p).

1. Alice selects a secret integer a and computes A = [a]P;

2. Bob selects a secret integer b and computes B = [b]P;

3. Alice and Bob exchange A and B;

4. Alice computes [a]B and Bob computes [b]A. Now they have the shared point [ab]P.

Elliptic Curve Digital Signature Algorithm (ECDSA)

Alice and Bob agree on a field \mathbb F_p, and elliptic curve E over the field \mathbb F_p, and a point P \in E(\mathbb F_p) of prime order N.

1. Alice selects a secret integer a and computes A = [a]P; this is her public key;

2. Alice randomly chooses another integer b \in [1, N-1];

3. Alice hashes her message and gets an integer d \pmod N;

4. Alice sets s_1 to be the x-coordinate of [b]P \pmod N;

5. Alice then computes s_2 \equiv (d+as_1)b^{-1}\pmod N;

6. Alice publishes s_1 and s_2;

7. To verify the signature, Bob computes v_1\equiv ds_2^{-1} \pmod N and v_2\equiv s_1s_2^{-1} \pmod N;

8. Bob then computes [v_1]P+[v_2]A; let g be the x-coordinate of this point. If Alice and Bob have the same message, then g \equiv s_1 \pmod N.

Elliptic Curve Encryption

Alice and Bob agree on a field \mathbb F_p, and elliptic curve E over the field \mathbb F_p, and a point P \in E(\mathbb F_p).

1. Alice selects a secret integer a and computes A = [a]P; a is the private key and A is the public key;

2. Bob randomly chooses an integer b. Assume the message Bob wants to encrypt is M;

3. Bob computes s_1 = [b]P and s_2 = M+[b]A;

4. Bob sends s_1, s_2 to Alice;

5. Alice obtains M by computing s_2-[a]s_1.